Estadistica

jueves, 14 de noviembre de 2013

Aplicación Estadística

Durante el siglo XX, la creación de instrumentos precisos para asuntos de salud pública (epidemiología, bioestadística, etc.) y propósitos económicos y sociales (tasa de desempleo, econometría, etc.) necesitó de avances sustanciales en las prácticas estadísticas.

Hoy el uso de la estadística se ha extendido más allá de sus orígenes como un servicio al Estado o al gobierno. Personas y organizaciones usan la estadística para entender datos y tomar decisiones en ciencias naturales y sociales, medicina, negocios y otras áreas. La estadística es entendida generalmente no como un sub-área de las matemáticas sino como una ciencia diferente «aliada». Muchas universidades tienen departamentos académicos de matemáticas y estadística separadamente. La estadística se enseña en departamentos tan diversos comopsicología, educación y salud pública.

Por razones prácticas, en lugar de compilar datos de una población entera, usualmente se estudia un subconjunto seleccionado de la población, llamado muestra. Datos acerca de la muestra son recogidos de manera observacional o experimental. Los datos son entonces analizados estadísticamente lo cual sigue dos propósitos: descripción e inferencia.Al aplicar la estadística a un problema científico, industrial o social, se comienza con un proceso o población a ser estudiado. Esta puede ser la población de un país, de granos cristalizados en una roca o de bienes manufacturados por una fábrica en particular durante un periodo dado. También podría ser un proceso observado en varios ascos instantes y los datos recogidos de esta manera constituyen una serie de tiempo.

El concepto de correlación es particularmente valioso. Análisis estadísticos de un conjunto de datos puede revelar que dos variables (esto es, dos propiedades de la población bajo consideración) tienden a variar conjuntamente, como si hubiera una conexión entre ellas. Por ejemplo, un estudio del ingreso anual y la edad de muerte podría resultar en que personas pobres tienden a tener vidas más cortas que personas de mayor ingreso. Las dos variables se dicen que están correlacionadas. Sin embargo, no se puede inferir inmediatamente la existencia de una relación de causalidad entre las dos variables. El fenómeno correlacionado podría ser la causa de una tercera, previamente no considerada, llamada variable confusora.

Si la muestra es representativa de la población, inferencias y conclusiones hechas en la muestra pueden ser extendidas a la población completa. Un problema mayor es el de determinar que tan representativa es la muestra extraída. La estadística ofrece medidas para estimar y corregir por aleatoriedad en la muestra y en el proceso de recolección de los datos, así como métodos para diseñar experimentos robustos como primera medida, ver diseño experimental.

El concepto matemático fundamental empleado para entender la aleatoriedad es el de probabilidad. La estadística matemática (también llamada teoría estadística) es la rama de las matemáticas aplicadas que usa la teoría de probabilidades y el análisis matemático para examinar las bases teóricas de la estadística.

El uso de cualquier método estadístico es válido solo cuando el sistema o población bajo consideración satisface los supuestos matemáticos del método. El mal uso de la estadística puede producir serios errores en la descripción e interpretación, afectando las políticas sociales, la práctica médica y la calidad de estructuras tales como puentes y plantas de reacción nuclear.

Incluso cuando la estadística es correctamente aplicada, los resultados pueden ser difícilmente interpretados por un inexperto. Por ejemplo, el significado estadístico de una tendencia en los datos, que mide el grado al cual la tendencia puede ser causada por una variación aleatoria en la muestra, puede no estar de acuerdo con el sentido intuitivo. El conjunto de habilidades estadísticas básicas (y el escepticismo) que una persona necesita para manejar información en el día a día se refiere como «cultura estadística».

Teoría de Conjuntos

La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.¹

Sin embargo, la teoría de los conjuntos es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones,figuras geométricas, ...; y junto con la lógica permite estudiar los fundamentos de esta. En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente para desarrollar toda la matemática.

Además, la propia teoría de conjuntos es objeto de estudio per se, no sólo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. En esta disciplina es habitual que se presenten casos de propiedades indemostrables o contradictorias, como la hipótesis del continuo o la existencia de un cardinal inaccesible. Por esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica matemática.

El desarrollo histórico de la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas «puras» del infinito en la segunda mitad delsiglo XIX, precedido por algunas ideas de Bernhard Bolzano e influenciado por Richard Dedekind. El descubrimiento de las paradojas de la teoría cantoriana, de conjuntos, formalizada por Gottlob Frege, propició los trabajos de Bertrand Russell, Ernst Zermelo, Abraham Fraenkel y otros a principios del siglo XX.

Teoría básica de conjuntos

La teoría de conjuntos más elemental es una de las herramientas básicas del lenguaje matemático. Dados unos elementos, unos objetos matemáticos como números o polígonos por ejemplo, puede imaginarse una colección determinada de estos objetos, un conjunto. Cada uno de estos elementos pertenece al conjunto, y esta noción de pertenencia es la relación relativa a conjuntos más básica. Los propios conjuntos pueden imaginarse a su vez como elementos de otros conjuntos. La pertenencia de un elemento a a un conjunto A se indica como a ∈ A.

Una relación entre conjuntos derivada de la relación de pertenencia es la relación de inclusión. Una subcolección de elementos B de un conjunto dado A es un subconjunto de A, y se indica como B ⊆ A.

Ejemplos.

Los conjuntos numéricos usuales en matemáticas son: el conjunto de los números naturales N, el de los números enteros Z, el de los números racionales Q, el de los números reales R y el de los números complejos C. Cada uno es subconjunto del siguiente:

$\mathbb{N}\subseteq\mathbb{Z}\subseteq\mathbb{Q}\subseteq\mathbb{R}\subseteq\mathbb{C}$

El espacio tridimensional E₃ es un conjunto de objetos elementales denominados puntos p, p ∈ E₃. Las rectas r y planos $α$ son conjuntos de puntos a su vez, y en particular son subconjuntos de E₃, r ⊆ E₃ y $α$ ⊆ E₃.

Álgebra de conjuntos

Existen unas operaciones básicas que permiten manipular los conjuntos y sus elementos, similares a las operaciones aritméticas, constituyendo el álgebra de conjuntos:

Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene cada elemento que está por lo menos en uno de ellos.
Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.
Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.
Complemento. El complemento de un conjunto A es el conjunto A^∁ que contiene todos los elementos (respecto de algún conjunto referencial) que no pertenecen a A.

Diferencia simétrica La diferencia simétrica de dos conjuntos A y B es el conjunto A Δ B con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento a pertenece a A y su segundo elemento b pertenece a B.

Teoría axiomática de conjuntos

La teoría informal de conjuntos apela a la intuición para determinar como se comportan los conjuntos. Sin embargo, es sencillo plantear cuestiones acerca de las propiedades de estos que llevan a contradicción si se razona de esta manera, como la famosa paradoja de Russell. Históricamente esta fue una de las razones para el desarrollo de las teorías axiomáticas de conjuntos, siendo otra el interés en determinar exactamente qué enunciados acerca de los conjuntos necesitan que se asuma el polémico axioma de elección para ser demostrados.

Las teorías axiomáticas de conjuntos son colecciones precisas de axiomas escogidos para poder derivar todas las propiedades de los conjuntos con el suficiente rigor matemático. Algunos ejemplos conocidos son:

La teoría de conjuntos de Zermelo-Fraenkel
La teoría de conjuntos de Neumann-Bernays-Gödel
La teoría de conjuntos de Morse-Kelley

Medidas de Tendencia Central

Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro de la distribución de datos se denomina medida oparámetro de tendencia central o de centralización. Cuando se hace referencia únicamente a la posición de estos parámetros dentro de la distribución, independientemente de que ésta esté más o menos centrada, se habla de estas medidas como medidas de posición.¹ En este caso se incluyen también los cuantiles entre estas medidas.

Entre las medidas de tendencia central tenemos:

Se debe tener en cuenta que existen variables cualitativas y variables cuantitativas, por lo que las medidas de posición o medidas de tendencia se usan de acuerdo al tipo de variable que se está observando, en este caso se observan variables cuantitativas.

La media aritmética

La media aritmética es el valor obtenido por la suma de todos sus valores dividida entre el número de sumandos.

Por ejemplo, las notas de 5 alumnos en una prueba:

niño     nota

 1       6,0    ·Primero, se suman las notas:
 2       5,4        6,0+5,4+3,1+7,0+6,1 = 27,6
 3       3,1    ·Luego el total se divide entre la cantidad de alumnos:
 4       7,0         27,6/5=5,52
 5       6,1

· La media aritmética en este ejemplo es 5,52

La media aritmética es, probablemente, uno de los parámetros estadísticos más extendidos.² Se le llama también promedio o, simplemente, media.

Definición formal

Dado un conjunto numérico de datos, x₁, x₂, ..., x_n, se define su media aritmética como

$\overline{x} = \frac{x_1 + x_2 + ... + x_n}{n} = \frac{\sum_{i=1}^n x_i}{n}$

Esta definición varía, aunque no sustancialmente, cuando se trata de variables continuas, esto es, también puede calcularse para variables agrupadas en intervalos.

Propiedades

Las principales propiedades de la media aritmética son:

Su cálculo es muy sencillo y en él intervienen todos los datos.

Su valor es único para una serie de datos dada.

Se usa con frecuencia para comparar poblaciones, aunque es más apropiado acompañarla de una medida de dispersión.

Se interpreta como "punto de equilibrio" o "centro de masas" del conjunto de datos, ya que tiene la propiedad de equilibrar las desviaciones de los datos respecto de su propio valor:

$\frac{\sum_{i=1}^n (x_i-\overline{x})}{n} = \frac{\sum_{i=1}^n x_i}{n} - \frac{\sum_{i=1}^n \overline{x}}{n} = \overline{x} - \overline{x} = 0$

Minimiza las desviaciones cuadráticas de los datos respecto de cualquier valor prefijado, esto es, el valor de $\frac{\sum_{i=1}^n (x_i-k)^2}{n}$ es mínimo cuando $k = \overline{x}$ . Este resultado se conoce como Teorema de König. Esta propiedad permite interpretar uno de los parámetros de dispersión más importantes: la varianza.

Se ve afectada por transformaciones afines (cambios de origen y escala), esto es, si

$x_i' = ax_i+b$ entonces $\overline{x'} = a \overline{x} + b$ , donde $\overline{x'}$ es la media aritmética de los $x_i'$ , para i = 1, ..., n y a y b números reales.

Es poco sensible a fluctuaciones muestrales, por lo que es un parámetro muy útil en inferencia estadística.

Inconvenientes de su uso

Este parámetro, aún teniendo múltiples propiedades que aconsejan su uso en situaciones muy diversas, tiene también algunos inconvenientes, como son:

Para datos agrupados en intervalos (variables continuas) su valor oscila en función de la cantidad y amplitud de los intervalos que se consideren.

La estatura media como resumen de una población homogénea (abajo) o heterogénea (arriba).

Es una medida a cuyo significado afecta sobremanera la dispersión, de modo que cuanto menos homogéneos sean los datos, menos información proporciona. Dicho de otro modo, poblaciones muy distintas en su composición pueden tener la misma media.⁴ Por ejemplo, un equipo de baloncesto con cinco jugadores de igual estatura, 1,95 m, evidentemente, tendría una estatura media de 1,95 m, valor que representa fielmente a esta población homogénea. Sin embargo, un equipo de jugadores de estaturas más heterogéneas, 2,20 m, 2,15 m, 1,95 m, 1,75 m y 1,70 m, por ejemplo, tendría también, como puede comprobarse, una estatura media de 1,95 m, valor que no representa a casi ninguno de sus componentes.

En el cálculo de la media no todos los valores contribuyen de la misma manera. Los valores altos tienen más peso que los valores cercanos a cero. Por ejemplo, en el cálculo del salario medio de un empresa, el salario de un alto directivo que gane 1.000.000 de € tiene tanto peso como el de diez empleados "normales" que ganen 1.000 €. En otras palabras, se ve muy afectada por valores extremos.

No se puede determinar si en una distribución de frecuencias hay intervalos de clase abiertos.

Media aritmética ponderada

A veces puede ser útil otorgar pesos o valores a los datos dependiendo de su relevancia para determinado estudio. En esos casos se puede utilizar una media ponderada.

Si $x_{1},x_{2},..., x_{n}$ son nuestros datos y $w_{1},w_{2},..., w_{n}$ son sus "pesos" respectivos, la media ponderada se define de la siguiente forma:

$\frac{x_{1}w_{1}+x_{2}w_{2}+ ...+x_{n}w_{n}}{w_{1}+w_{2}+ ...+w_{n}}$

Media muestral

Esencialmente, la media muestral es el mismo parámetro que el anterior, aunque el adjetivo "muestral" se aplica a aquellas situaciones en las que la media aritmética se calcula para un subconjunto de la población objeto de estudio.

La media muestral es un parámetro de extrema importancia en la inferencia estadística, siendo de gran utilidad para la estimación de la media poblacional, entre otros usos.

Moda

La moda es el dato más repetido, el valor de la variable con mayor frecuencia absoluta.⁵ En cierto sentido la definición matemática corresponde con la locución "estar de moda", esto es, ser lo que más se lleva.

Su cálculo es extremadamente sencillo, pues sólo necesita un recuento. En variables continuas, expresadas en intervalos, existe el denominado intervalo modal o, en su defecto, si es necesario obtener un valor concreto de la variable, se recurre a la interpolación.

Por ejemplo, el número de personas en distintos vehículos en una carretera: 5-7-4-6-9-5-6-1-5-3-7. El número que más se repite es 5, entonces la moda es 5.

Hablaremos de una distribución bimodal de los datos, cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Cuando en una distribución de datos se encuentran tres o más modas, entonces es multimodal. Por último, si todas las variables tienen la misma frecuencia diremos que no hay moda.

Cuando tratamos con datos agrupados en intervalos, antes de calcular la moda, se ha de definir el intervalo modal. El intervalo modal es el de mayor frecuencia absoluta.

La moda, cuando los datos están agrupados, es un punto que divide el intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:

$\frac{p}{c-p}=\frac{n_i-n_{i-1} }{n_i-n_{i+1} }$

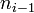
Siendo $n_{i}$ la frecuencia absoluta del intervalo modal y $n_{i-1}$ y $n_{i+1}$ las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al intervalo modal.

Las calificaciones en la asignatura de Matemáticas de 39 alumnos de una clase viene dada por la siguiente tabla (debajo):

Calificaciones	1	2	3	4	5	6	7	8	9
Número de alumnos	2	2	4	5	8	9	3	4	2

Propiedades

Sus principales propiedades son:

Cálculo sencillo.
Interpretación muy clara.
Al depender sólo de las frecuencias, puede calcularse para variables cualitativas. Es por ello el parámetro más utilizado cuando al resumir una población no es posible realizar otros cálculos, por ejemplo, cuando se enumeran en medios periodísticos las características más frecuentes de determinado sector social. Esto se conoce informalmente como "retrato robot".⁶

Inconvenientes

Su valor es independiente de la mayor parte de los datos, lo que la hace muy sensible a variaciones muestrales. Por otra parte, en variables agrupadas en intervalos, su valor depende excesivamente del número de intervalos y de su amplitud.
Usa muy pocas observaciones, de tal modo que grandes variaciones en los datos fuera de la moda, no afectan en modo alguno a su valor.
No siempre se sitúa hacia el centro de la distribución.
Puede haber más de una moda en el caso en que dos o más valores de la variable presenten la misma frecuencia (distribuciones bimodales o multimodales).

Mediana

La mediana es un valor de la variable que deja por debajo de sí a la mitad de los datos, una vez que éstos están ordenados de menor a mayor.⁷ Por ejemplo, la mediana del número de hijos de un conjunto de trece familias, cuyos respectivos hijos son: 3, 4, 2, 3, 2, 1, 1, 2, 1, 1, 2, 1 y 1, es 2, puesto que, una vez ordenados los datos: 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, el que ocupa la posición central es 2:

$\rm \underbrace{1,\ 1,\ 1,\ 1,\ 1,\ 1, }_{Mitad \; inferior} \; \underbrace{\color{Red} 2, }_{Mediana \;} \; \underbrace{2,\ 2,\ 2,\ 3,\ 3,\ 4}_{Mitad \; superior}$

En caso de un número par de datos, la mediana no correspondería a ningún valor de la variable, por lo que se conviene en tomar como mediana el valor intermedio entre los dos valores centrales. Por ejemplo, en el caso de doce datos como los siguientes:

$\rm \underbrace{1,\ 1,\ 1,\ 1,\ 1, }_{Valores \; inferiores} \; \underbrace{\color{Red} 1,\ 2, }_{Valores \; intermedios} \; \underbrace{2,\ 2,\ 3,\ 3,\ 4}_{Valores \; superiores}$

Se toma como mediana $1,5 = \frac{{\color{Red}1}+{\color{Red}2}}{2}$

Existen métodos de cálculo más rápidos para datos más númerosos (véase el artículo principal dedicado a este parámetro). Del mismo modo, para valores agrupados en intervalos, se halla el "intervalo mediano" y, dentro de éste, se obtiene un valor concreto por interpolación.

Cálculo de la mediana para datos agrupados

Primero hallamos las frecuencias absolutas acumuladas Fi (ver tabla del margen derecho).

Así, aplicando la formula asociada a la mediana para n impar, obtenemos X(39+1)/2 = X20 y basándonos en la fórmula que hace referencia a las frecuencias absolutas:

N_i-1< n/2 < _i = N19 < 19.5 < N20

Por tanto la mediana será el valor de la variable que ocupe el vigésimo lugar. En nuestro ejemplo, 21 (frecuencia absoluta acumulada para X_i = 5) > 19.5 con lo que M_e = 5 puntos (es aconsejable no olvidar las unidades; en este caso como estamos hablando de calificaciones, serán puntos)

La mitad de la clase ha obtenido un 5 o menos, y la otra mitad un 5 o más.

Ejemplo (N par)

Las calificaciones en la asignatura de Matemáticas de 38 alumnos de una clase viene dada por la siguiente tabla (debajo):

Calificaciones	1	2	3	4	5	6	7	8	9
Número de alumnos	2	2	4	5	6	9	4	4	2

x_i	f_i	F_i
1	2	2
2	2	4
3	4	8
4	5	13
5	6	19 = 19
6	9	28
7	4	32
8	4	36
9	2	38

Calculemos la Mediana:

Primero hallamos las frecuencias absolutas acumuladas F_i (ver tabla margen derecho).

Si volvemos a utilizar la fórmula asociada a la mediana para n par, obtenemos X(38/2) = X19 y basándonos en la fórmula que hace referencia a las frecuencias absolutas --> N_i-1< n/2 < N_i = N18 < 19 < N19

Con lo cual la mediana será la media aritmética de los valores de la variable que ocupen el decimonoveno y el vigésimo lugar.

En nuestro ejemplo, el lugar decimonoveno lo ocupa el 5 y el vigésimo el 6, (desde el vigésimo hasta el vigésimo octavo)

con lo que M_e = (5+6)/2 = 5,5 puntos.

Propiedades e inconvenientes

Las principales propiedades de la mediana son:

Es menos sensible que la media a oscilaciones de los valores de la variable. Un error de transcripción en la serie del ejemplo anterior en, pongamos por caso, el último número, deja a la mediana inalterada.
Como se ha comentado, puede calcularse para datos agrupados en intervalos, incluso cuando alguno de ellos no está acotado.
No se ve afectada por la dispersión. De hecho, es más representativa que la media aritmética cuando la población es bastante heterogénea. Suele darse esta circunstancia cuando se resume la información sobre los salarios de un país o una empresa. Hay unos pocos salarios muy altos que elevan la media aritmética haciendo que pierda representatividad respecto al grueso de la población. Sin embargo, alguien con el salario "mediano" sabría que hay tanta gente que gana más dinero que él, como que gana menos.

Sus principales inconvenientes son que en el caso de datos agrupados en intervalos, su valor varía en función de la amplitud de estos. Por otra parte, no se presta a cálculos algebraicos tan bien como la media aritmética.

Medidas de Dispersión

Las medidas de dispersión, también llamadas medidas de variabilidad, muestran la variabilidad de una distribución, indicando por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la mediana media.Cuánto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la mediana media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos.

Para calcular la variabilidad que una distribución tiene respecto de su media, se calcula la media de las desviaciones de las puntuaciones respecto a la media aritmética. Pero la suma de las desviaciones es siempre cero, así que se adoptan dos clases de estrategias para salvar este problema. Una es tomando las desviaciones en valor absoluto (Desviación media) y otra es tomando las desviaciones al cuadrado (Varianza).

Rango estadístico

El rango o recorrido estadístico es la diferencia entre el valor máximo y el valor mínimo en un grupo de números aleatorios. Se le suele simbolizar con R.

Requisitos del rango

Ordenamos los números según su tamaño.
Restamos el valor mínimo del valor máximo

$Rango = {(Max - Min)}$

Ejemplo

Para una muestra (8,7,6,9,4,5), el dato menor es 4 y el dato mayor es 9 (Valor unitario inmediatamente posterior al dato mayor menos el dato menor). Sus valores se encuentran en un rango de:

$Rango = (9-4) = 5$

Medio rango o Rango medio

El medio rango o rango medio de un conjunto de valores numéricos es la media del mayor y menor valor, o la tercera parte del camino entre el dato de menor valor y el dato de mayor valor. En consecuencia, el medio rango es:

$medioRango = \frac{\ (Max + Min)}{2}$

Ejemplo

Para una muestra de valores (3, 3, 5, 6, 8), el dato de menor valor Min= 3 y el dato de mayor valor Max= 8. El medio rango resolviéndolo mediante la correspondiente fórmula sería:

$medioRango = \frac{\ (3 + 8)}{2} = 5.5$

Representación del medio rango:

Varianza

La varianza es una medida estadística que mide la dispersión de los valores respecto a un valor central (media), es decir, es el cuadrado de las desviaciones: $S_X^2 = \frac{\sum_{i=1}^n (X_i - \bar{X})^2}{n-1}$

$S_X^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2$

Propiedades

La varianza es siempre positiva o 0: $V_{X}^2 \geq 0$
Si a los datos de la distribución les sumamos una cantidad constante la varianza no se modifica.

$Y_i = X_i + k$ ¹ c $S_Y^2 = \frac{\sum (Y_i - \bar{Y})^2}{n} = \frac{\sum [(X_i + k) - (\bar{X} + k)]^2}{n} = \frac{\sum (X_i + k - \bar{X} - k)^2}{n} = \frac{\sum (X_i - \bar{X})^2}{n} = S_X^2$

Si a los datos de la distribución los multiplicamos una constante, la varianza queda multiplicada por el cuadrado de esa constante.

$Y_i = X_i \cdot k$

$S_Y^2 = \frac{\sum (Y_i - \bar{Y})^2}{n} = \frac{\sum (X_i \cdot k - \bar{X} \cdot k)^2}{n} = \frac{\sum [k \cdot (X_i - \bar{X})]^2}{n} = \frac{\sum [k^2 \cdot (X_i - \bar{X})^2]}{n} = k^2 \cdot \frac{\sum (X_i - \bar{X})^2}{n} = k^2 \cdot S_X^2$

Propiedad distributiva: $V(X + Y) = V(X) + V(Y) -$ cov $(X,Y)$

Desviación típica

La varianza a veces no se interpreta claramente, ya que se mide en unidades cuadráticas. Para evitar ese problema se define otra medida de dispersión, que es la desviación típica, o desviación estándar, que se halla como la raíz cuadrada positiva de la varianza. La desviación típica informa sobre la dispersión de los datos respecto al valor de la media; cuanto mayor sea su valor, más dispersos estarán los datos. Esta medida viene representada en la mayoría de los casos por S, dado que es su inicial de su nominación en inglés.

Desviación típica muestral

$S = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n}}$

Desviación típica poblacional

$\sigma = \sqrt{\frac{\sum_{i=1}^n fi (X_i - \mu)^2}{n}}$

-->x = [17 14 2 5 8 7 6 8 5 4 3 15 9]
x = 17. 14. 2. 5. 8. 7. 6. 8. 5. 4. 3. 15. 9.
-->stdev(x)
ans = 4.716311
-->

Primero hemos declarado un vector con nombre X, donde introduzco los números de la serie. Luego con el comando stdev se hallará la desviación típica.

Covarianza

La covarianza entre dos variables es un estadístico resumen indicador de si las puntuaciones están relacionadas entre sí. La formulación clásica, se simboliza por la letra griega sigma (σ) cuando ha sido calculada en la población. Si se obtiene sobre una muestra, se designa por la letra " $s_{xy}$ ".

La fórmula suele aparecer expresada como:

$\hat{S}_{xy} = \frac{\sum_{i=1}^n x_i y_i}{n-1} = \frac{\sum_{i=1}^n (X_i - \bar{X})(Y_i - \bar{Y})}{n-1}$

Este tipo de estadístico puede utilizarse para medir el grado de relación de dos variables si ambas utilizan una escala de medida a nivel de intervalo/razón (variables cuantitativas).

La expresión se resuelve promediando el producto de las puntuaciones diferenciales por su tamaño muestral (n pares de puntuaciones, n-1 en su forma insesgada).

Este estadístico, refleja la relación lineal que existe entre dos variables. El resultado numérico fluctúa entre los rangos de +infinito a -infinito. Al no tener unos límites establecidos no puede determinarse el grado de relación lineal que existe entre las dos variables, solo es posible ver la tendencia.

$-\infty \leq S_{xy} \leq +\infty$
$S_{xy} = \begin{cases} > 0, & \mbox{Correlaci}\acute{o}\mbox{n directa. Recta de regresi}\acute{o}\mbox{n creciente.} \\ = 0, & \mbox{No hay correlaci}\acute{o}\mbox{n.} \\ < 0. & \mbox{Correlaci}\acute{o}\mbox{n inversa. Recta de regresi}\acute{o}\mbox{n decreciente.} \end{cases}$

Coeficiente de Correlación de Pearson

El coeficiente de correlación de Pearson, r, permite saber si el ajuste de la nube de puntos a la recta de regresión obtenida es satisfactorio. Se define como el cociente entre la covarianza y el producto de las desviaciones típicas (raíz cuadrada de las varianzas).

$r = \frac{V_{xy}}{\sqrt{V_x V_y}} = \frac{S_{xy}}{\sqrt{S_x^2 S_y^2}} = \frac{S_{xy}}{S_x S_y}$

Teniendo en cuenta el valor de la covarianza y las varianzas, se puede evaluar mediante cualquiera de las dos expresiones siguientes:

Ejemplo Para una muestra de valores (3, 3, 5, 6, 8), el dato de menor valor Min= 3 y el dato de mayor valor Max= 8. El medio rango resolviéndolo mediante la correspondiente fórmula sería: $r = \frac{\frac{\sum x_i y_i}{n} - \bar{x}\bar{y}} {\sqrt{\left(\frac{\sum x_i^2}{n} - \bar{x}^{2}\right) \left(\frac{\sum y_i^2}{n} - \bar{y}^{2}\right)}}$

$r = \frac{n\sum x_i y_i - \sum x_i \sum y_i} {\sqrt{\left[n\sum x_i^2 - \left(\sum x_i\right)^2\right] \left[n\sum y_i^2 - \left(\sum y_i\right)^2\right]}}$

Propiedades

El coeficiente de correlación, r, presenta valores entre –1 y +1.
Cuando r es próximo a 0, no hay correlación lineal entre las variables. La nube de puntos está muy dispersa o bien no forma una línea recta. No se puede trazar una recta de regresión.
Cuando r es cercano a +1, hay una buena correlación positiva entre las variables según un modelo lineal y la recta de regresión que se determine tendrá pendiente positiva, será creciente.
Cuando r es cercano a -1, hay una buena correlación negativa entre las variables según un modelo lineal y la recta de regresión que se determine tendrá pendiente negativa: es decreciente.es